间隔分析
#1 概述
间隔分析是分析用户产生两个指定事件之间的时间间隔的分析模型,通过间隔分析模型,分析人员观察用户完成两次指定事件的时间间隔的分布情况,了解用户某一核心行为的发生频率,或者获取两个具有前后因果关系的事件的转化时长。
间隔分析既可以用于统计产品的登录时间间隔、复购周期等,作为衡量用户活跃度和用户黏性的分析工具;也可以作为对转化漏斗分析的一种补充,通过转化时长指标来衡量特定转化路径在时间维度上的转化效率。
#2 功能介绍
#2.1 整体界面
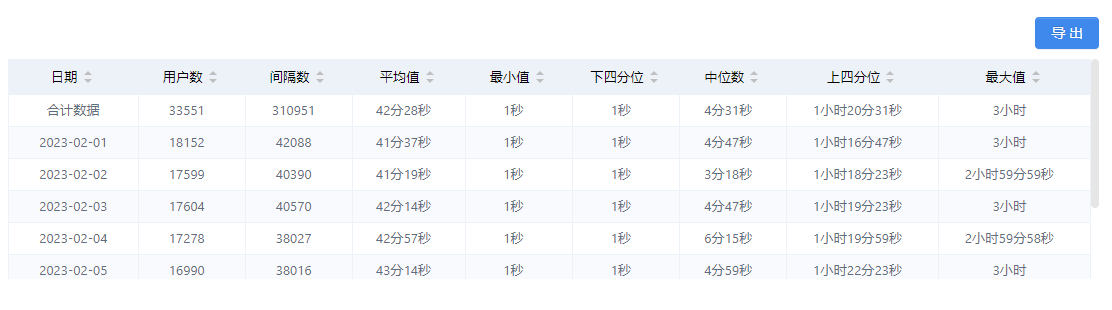
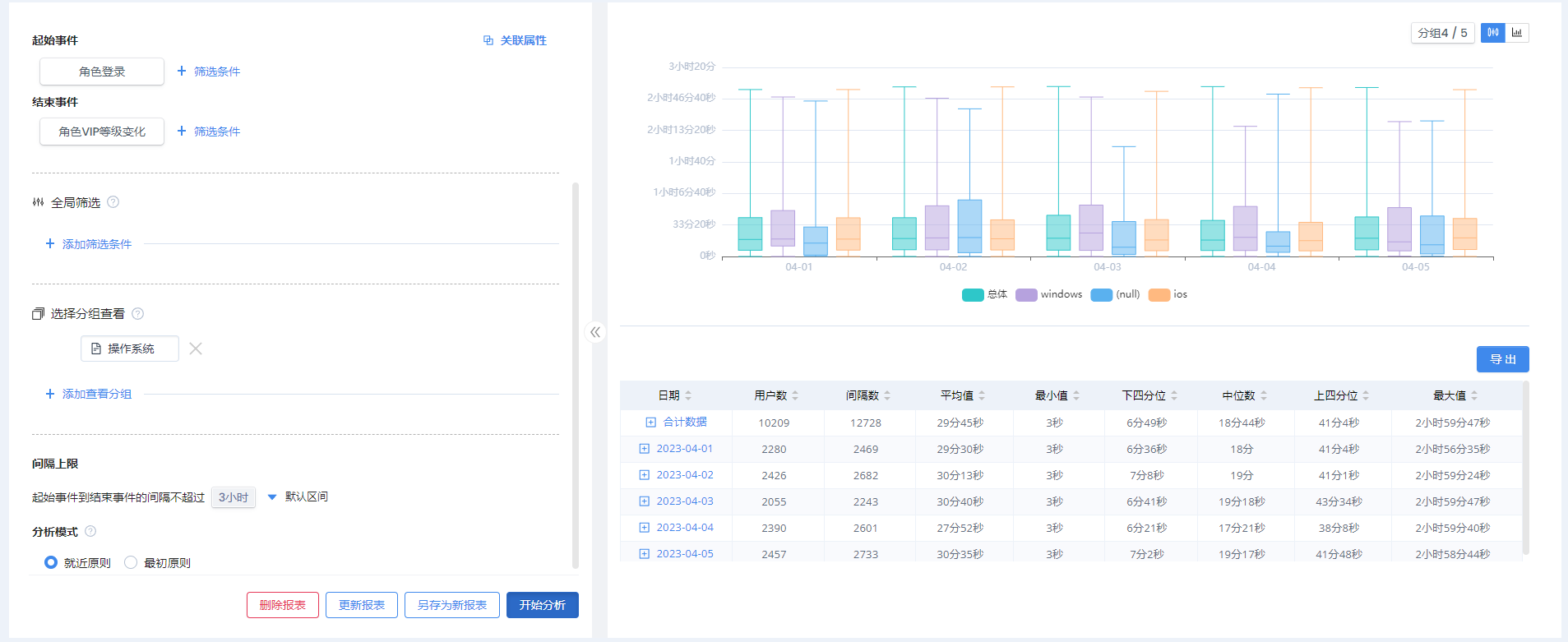
左侧为条件筛选区域,添加起始事件和结束事件,选择区间类型及筛选条件进行查询。右侧为查询结果展示区域,默认展示盒须图和数据表。
#2.2 起始事件和结束事件
选择起始事件和结束事件,可以选择同一事件,也可以选择不同的事件;
 例如:可以将起始事件和结束事件设置为 [app启动],用于计算用户两次进行app启动的时间间隔;将起始事件和结束事件设置为 [支付成功] ,用来统计用户复购周期。
例如:可以将起始事件和结束事件设置为 [app启动],用于计算用户两次进行app启动的时间间隔;将起始事件和结束事件设置为 [支付成功] ,用来统计用户复购周期。
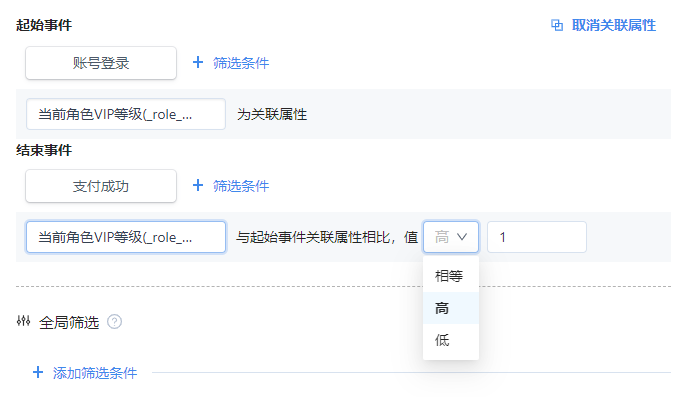
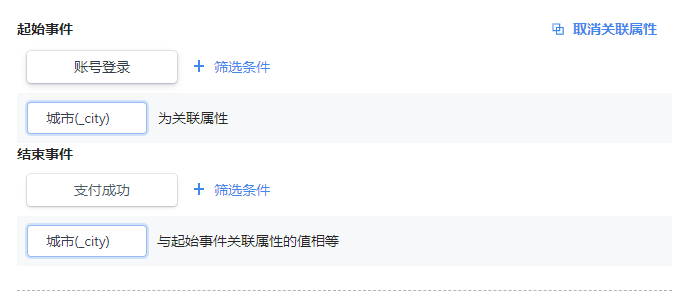
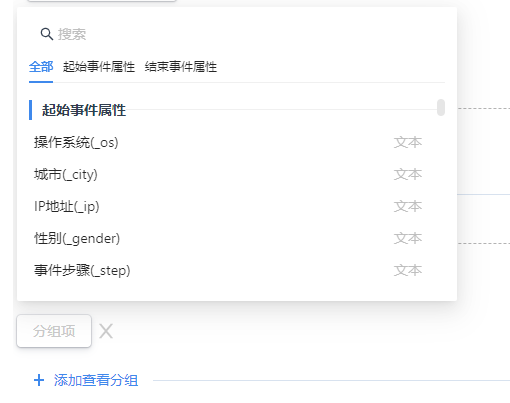
关联属性:设置起始事件和结束事件的关联属性,两个事件的关联属性可以不同,但属性类型需要一致。所有类型都可以选择两个关联属性相等,数值型属性还可以在结束事件下方设置属性值高于或低于多少值。
假设我们查看用户从[账号登录]到[支付成功]的时间间隔,若用户在不同城市触发了这两个行为,都会被统计在内。设置关联属性为[城市],则起始事件和结束事件发生时,用户[城市]属性必须一致,若用户在A城市进行[账号登录],在B城市进行了[支付成功],该查询结果不符合当前的指标值,不展示在查询结果区。
#2.3 条件筛选
支持进行筛选的属性数据类型包括:文本类型、数值类型、布尔类型、时间类型;
文本类型的属性可选逻辑关系为:
-
包含:所输入的值与属性值整个字符串完全一致则视为符合筛选条件
-
不包含:所输入的值与属性值某部分字符串不相同则视为符合筛选条件
-
等于:所输入的值与属性值整个字符串完全一致则视为符合筛选条件
-
不等于:所输入的值与属性值整个字符串不相同的视为符合筛选条件
-
有值:属性值不为空
-
无值:属性值为空
-
正则匹配:属性值满足正则表达式的匹配规则
-
正则不匹配:属性值不满足正则表达式的匹配规则
数值类型的属性可选逻辑关系为:
-
等于:可输入多个值,等于其中任意一个则视为符合筛选条件
-
不等于:可输入多个值,该属性有值且不等于其中任意一个视为符合筛选条件
-
小于:小于所输入的值视为符合筛选条件
-
大于:大于所输入的值视为符合筛选条件
-
大于等于:大于或等于所输入的值视为符合筛选条件
-
小于等于:小于或等于所输入的值视为符合筛选条件
-
区间:所输入的值为一个开区间,属性值在区间范围内视为符合筛选条件
-
有值:属性值不为空
-
无值:属性值为空
布尔类型的属性可选逻辑关系为:为真、为假。
-
为真:该属性为True视为符合筛选条件
-
为假:该属性为False视为符合筛选条件
-
有值:属性值不为空
-
无值:属性值为空
时间类型的属性可选逻辑关系为:
-
大于等于:属性值不早于设定的时间
-
小于等于:属性值不晚于设定的时间
-
区间:属性值在设置的时间区间范围内(区间为左闭右闭)
-
相对当前日期:将属性值与当前的日期进行比较
-
相对事件日期:将属性值与事件时间进行比较
-
有值:属性值不为空
-
无值:属性值为空
#2.4 分组查看
通过添加指标的分组,分析事件不同维度。例如添加城市分组,可查看不同城市用户带来的事件转化。
分组查看选择事件属性,可选择开始事件的属性分组 或 结束事件的属性分组
关联属性与分组的引入,都不会改变所有计算的核心逻辑。这两个功能在逻辑上比较类似,但处理上有所不同。关联属性的引入会在间隔计算前进行,首先会将所有原始数据按照关联属性进行分组,然后在各组内进行间隔的计算。而分组项则是在间隔计算完成后,再进行的间隔数据分组。由于进行分组的时刻不同且互不干扰,关联属性与分组也可以同时使用。
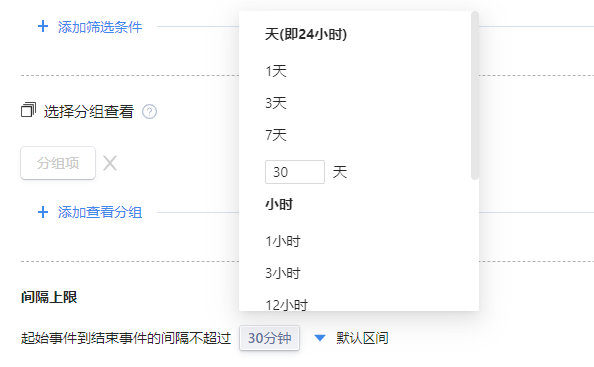
#2.5 间隔上限
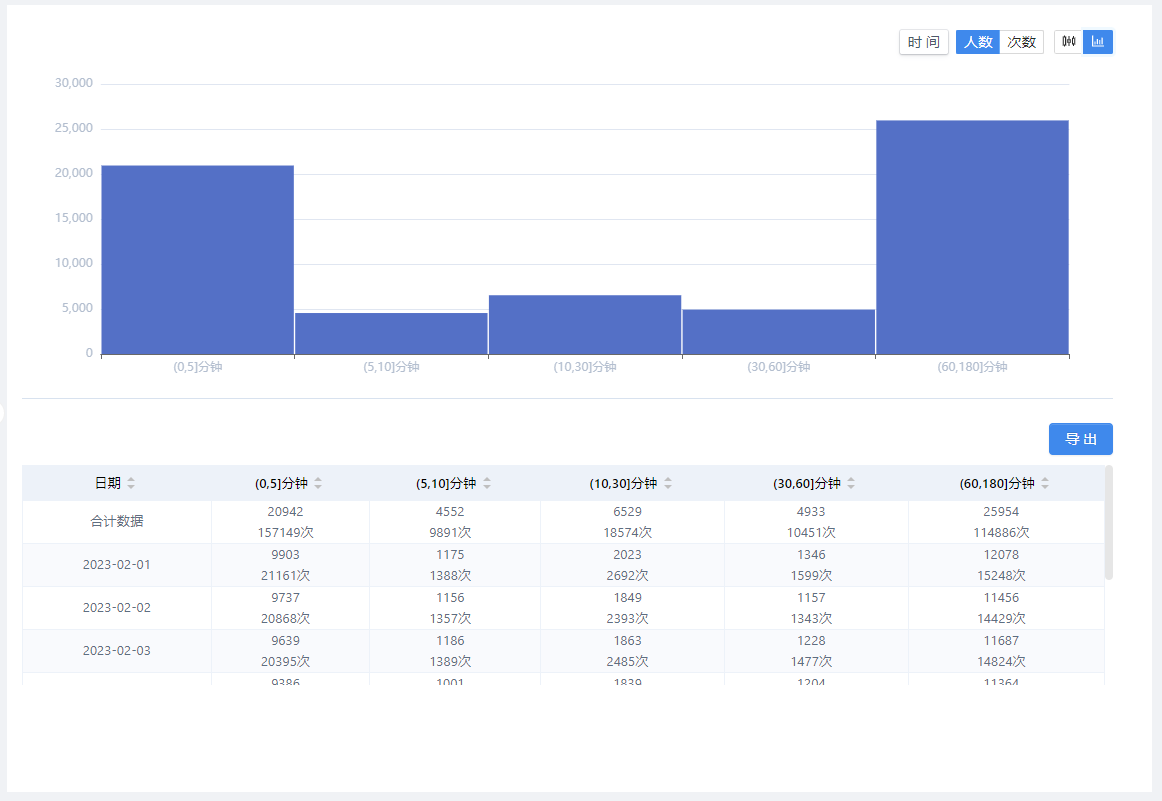
选择起始事件到结束事件的间隔上限时间,即所选择的两个事件发生的间隔时间不超过此间隔上限;可选择天、小时、分钟。
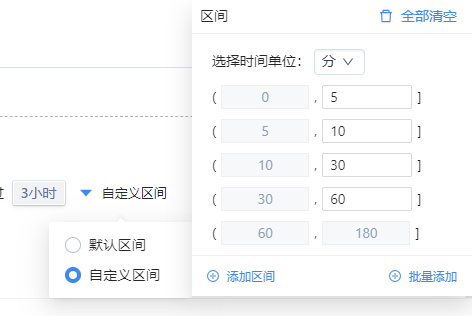
同时,还可以自定义间隔区间:
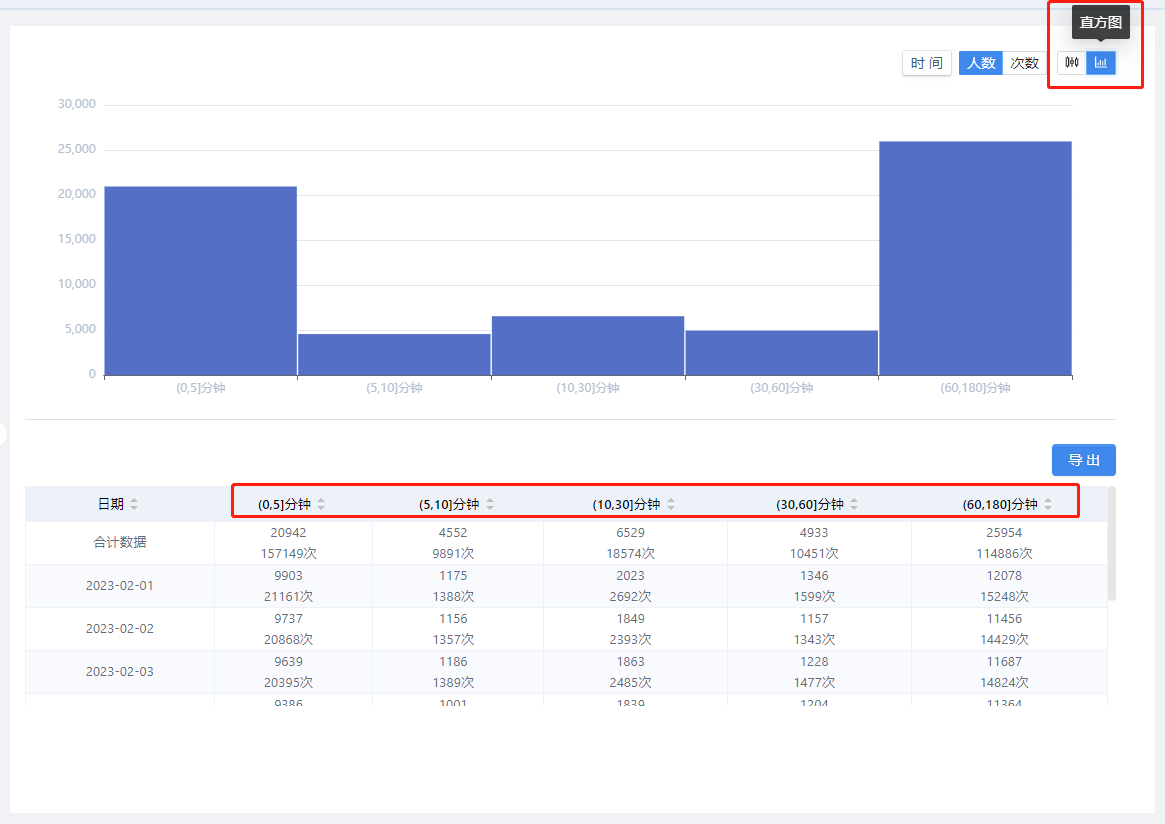
将所选择的间隔上限时间按特定的时间单位进行划分区间,切换至直方图即可查看区间结果;
#2.6 就近原则和最初原则
当起始事件为A,结束事件为B,且B事件都发生在间隔时间上限中,发生了已下情形:
| A | A | B | B | A | B | A | A | B |
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
选择就近原则和最初原则再次对间隔进行筛选,确保间隔与间隔不交叉; 就近原则:取起始事件与结束事件间隔时间最小的为基准,所得到的结果为:23 56 89 最初原则:取起始事件第一次发生时为基准找到第一次出现的结束事件,所得到的结果为:13 56 79